Introduction
Les structures de données permettent de stocker des données en mémoire de manière structurée et organisée ou bien d’avoir accès à des données . L’important dans le choix d’une structure de données, c’est de s’assurer d’avoir les fonctionnalités nécessaires, de manière efficace, mais sans laisser trop de liberté. En effet, plus on donne d’accès lors de l’utilisation d’une structure de données, plus le risque de problématique augmente.
Les différentes structures abstraites et leurs implémentations
Une structure abstraite est une version logique d’une structure de données, sans prendre en compte l’implémentation de cette dernière.
Une structure de donnée (non abstraite) consiste en l’implémentation de ces structures abstraites.
Les indexables
Une structure indexable est une structure abstraite de données qui permette d’accéder à une valeur en utilisant un index. L’index peut être numérique (comme dans un tableau) ou autre (comme dans une table de hachage).
Il est à noter que le langage Java n’a pas de classe abstraite représentant ce type de structure (et c’est malheureusement un manque dans la librairie Java).
Le langage Eiffel contient une classe abstraite « INDEXABLE » représentant ce type de structure. Vous pouvez voir la documentation ici.
Voici un exemple d’utilisation un objet « INDEXABLE » en Eiffel:
print_from_indexable(a_indexable:INDEXABLE[STRING, INTEGER])
-- Affiche les éléments de `a_indexable'
local
l_index:INTEGER
do
from l_index := a_indexable.lower until l_index > a_indexable.upper loop
print("Valeur a l'index " + l_index.out + ": " +
a_indexable.at (l_index) + "%N")
l_index := l_index + 1
end
end
Pour tester ce code, vous pouvez y envoyer n’importe quelle variable ayant un type conforme « INDEXABLE ». Voici un exemple simple:
make
-- Exécute l'exemple
local
l_liste:ARRAYED_LIST[STRING]
do
create l_liste.make(10)
l_liste.extend ("Element 1")
l_liste.extend ("Element 2")
l_liste.extend ("Element 3")
l_liste.extend ("Element 4")
l_liste.extend ("Element 5")
l_liste.extend ("Element 6")
l_liste.extend ("Element 7")
l_liste.extend ("Element 8")
l_liste.extend ("Element 9")
l_liste.extend ("Element 10")
print_from_indexable(l_liste)
end
Les itérables
Un itérable (parfois appelé traversable) est une structure abstraite avec laquelle il est possible de visiter chaque élément de la structure une unique fois.
En pratique, dans les langages, ce type de structure retourne un itérateur puisqu’un itérateur sert précisément à effectuer le travail indiqué plus haut. Vois le patron conceptuel « iterateur » dans la page de théorie précédente.
La documentation de l’interface « Iterable » en Java est ici
La documentation Eiffel de la classe « ITERABLE » est Eiffel est ici
Voici un exemple d’utilisation en Java:
/**
* Affiche les éléments d'un objet Iterable.
*
* @param aIterable L'objet contenant les éléments à afficher.
*/
public void printIterable(Iterable<String> aIterable) {
Iterator<String> lIterateur = aIterable.iterator();
while(lIterateur.hasNext()){
System.out.println(lIterateur.next());
}
}
Pour tester ce code, vous pouvez y envoyer n’importe quelle variable ayant un type conforme à « Iterable ». Voici un exemple simple:
/**
* Exécution de l'exemple.
*/
public void execute(){
List<String> lListe = new ArrayList<String>(10);
lListe.add("Element 1");
lListe.add("Element 2");
lListe.add("Element 3");
lListe.add("Element 4");
lListe.add("Element 5");
lListe.add("Element 6");
lListe.add("Element 7");
lListe.add("Element 8");
lListe.add("Element 9");
lListe.add("Element 10");
printIterableFor(lListe);
}
Voici un exemple en Eiffel (noter qu’en Eiffel, un itérateur est appelé curseur):
print_from_iterable(a_iterable:ITERABLE[STRING])
-- Affiche les éléments de `a_iterable'
local
l_iterateur:ITERATION_CURSOR[STRING]
do
l_iterateur := a_iterable.new_cursor
from until l_iterateur.after loop
print(l_iterateur.item + "%N")
l_iterateur.forth
end
end
Pour tester ce code, vous pouvez y envoyer n’importe quelle variable ayant comme type une classe implémentant « ITERABLE ». Voici un exemple simple:
make
-- Exécute l'exemple
local
l_liste:ARRAYED_LIST[STRING]
do
create l_liste.make(10)
l_liste.extend ("Element 1")
l_liste.extend ("Element 2")
l_liste.extend ("Element 3")
l_liste.extend ("Element 4")
l_liste.extend ("Element 5")
l_liste.extend ("Element 6")
l_liste.extend ("Element 7")
l_liste.extend ("Element 8")
l_liste.extend ("Element 9")
l_liste.extend ("Element 10")
print_from_iterable(l_liste)
end
Il est également à noter que, autant en Java qu’en Eiffel, l’objet « Iterable » est le type le plus abstrait pour lequel il est possible d’utiliser dans une boucle « for » (ou « across » en Eiffel). Par exemple, voici un exemple en Java utilisant un « for »:
/**
* Affiche les éléments d'un objet Iterable en utilisant "for".
*
* @param aIterable L'objet contenant les éléments à afficher.
*/
public void printIterable(Iterable<String> aIterable) {
for(String laElement:aIterable){
System.out.println(laElement);
}
}
Et voici un exemple en Eiffel:
print_from_iterable(a_iterable:ITERABLE[STRING])
-- Affiche les éléments de `a_iterable' avec une boucle "across"
do
across a_iterable as la_iterable loop
print(la_iterable.item + "%N")
end
end
Les deux exemples (Java et Eiffel) peuvent utiliser le même code d’exécution que présenté plus haut (les exemples avec les itérateurs).
Les tableaux
Un tableau (ou « array ») est une structure indexable et itérable dont la taille est fixe. L’index d’un tableau doit être numérique et continue, entre deux bornes (index minimal et index maximal).
Il est à noter qu’en Java, les tableaux (« array ») sont considérés comme des types primitifs et ne sont donc pas des classes ou des interfaces. Il est donc à déduire que les tableaux en Java n’implémentent pas « Iterable » et « Indexable ». Il n’y a également aucune documentation pour les tableaux en Java. Le tutoriel d’utilisation est ici.
La documentation de la classe « ARRAY » en Eiffel est ici.
Voici un exemple de tableau en Java:
/**
* Affiche les éléments d'un tableau.
*
* @param aTableau La structure contenant les éléments à afficher.
*/
public void printTableau(String[] aTableau) {
for(int i = 0; i < aTableau.length; i = i + 1){
System.out.println(aTableau[i]);
}
}
On utilise cet exemple en envoyant un tableau de « String » à la méthode:
/**
* Exécution de l'exemple.
*/
public void execute(){
String[] lTableau = new String[10];
lTableau[0] = "Element 1";
lTableau[1] = "Element 2";
lTableau[2] = "Element 3";
lTableau[3] = "Element 4";
lTableau[4] = "Element 5";
lTableau[5] = "Element 6";
lTableau[6] = "Element 7";
lTableau[7] = "Element 8";
lTableau[8] = "Element 9";
lTableau[9] = "Element 10";
printTableau(lTableau);
}
Voici un exemple de « ARRAY » en Eiffel:
print_from_array(a_array:ARRAY[STRING])
-- Affiche les éléments de `a_array'"
local
l_index:INTEGER
do
from l_index := a_array.lower until l_index > a_array.upper loop
print("Valeur a l'index " + l_index.out + ": " +
a_array.at (l_index) + "%N")
l_index := l_index + 1
end
end
Pour utiliser cet exemple, envoyer une variable ayant un type conforme à « ARRAY » en argument. Voici un exemple simple:
make
-- Exécute l'exemple
local
l_array:ARRAY[STRING]
do
create l_array.make_filled("", 1, 10)
l_array[1] := "Element 1"
l_array[2] := "Element 2"
l_array[3] := "Element 3"
l_array[4] := "Element 4"
l_array[5] := "Element 5"
l_array[6] := "Element 6"
l_array[7] := "Element 7"
l_array[8] := "Element 8"
l_array[9] := "Element 9"
l_array[10] := "Element 10"
print_from_array(l_array)
end
Les listes
On appel liste, une structure abstraite indexable et itérable ayant la possibilité de changer de taille. L’index d’une liste doit être numérique et continue, entre deux bornes (index minimal et index maximal).
La documentation de l’interface « List » de Java est ici
La documentation de la classe « LIST » de Eiffel est ici
Les listes tableau
Une liste tableau (ou « Array List ») est une liste implémentée à l’aide d’un tableau mémoire (« Array »). L’avantage d’une liste tableau est qu’elle permet d’accéder très rapidement à n’importe quel élément de la liste (ordre de complexité O(1)).
Le grand défaut d’une liste tableau, c’est que, comme vu plus haut, un tableau mémoire est toujours de taille fixe. Donc, qu’afin de pouvoir modifier la taille de la liste, le tableau au complet doit être copié dans un nouveau tableau d’une taille acceptable (ce qui est d’ordre de complexité O(n)). Avec optimisation, il est possible de réduire cette complexité à O(logn).
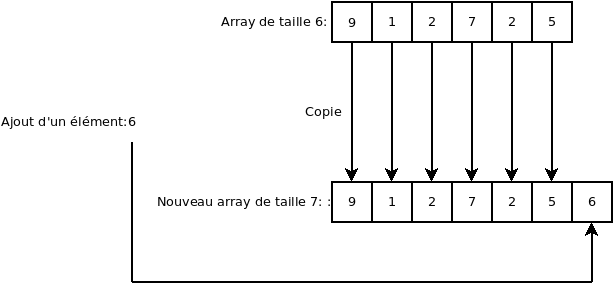
Il est important de noter que le tableau n’est pas nécessairement de la même taille que la liste. En effet, si on retire des éléments de la liste, la capacité du tableau n’est pas nécessairement réduite et lorsqu’on ajoute un élément dans la liste, le tableau n’est pas obligatoirement agrandit de 1 seul élément.
Nous obtenons donc que la liste a une taille (qui correspond au nombre d’éléments réellement placé dans la liste) et une capacité (qui correspond à au nombre d’éléments que le tableau interne peut recevoir).
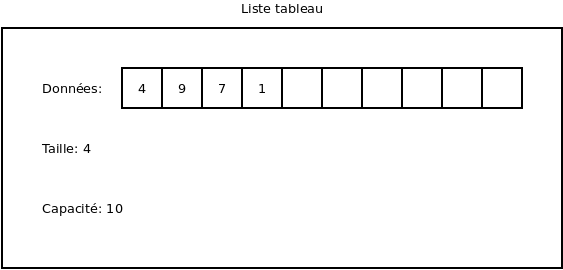
Il est à noter que, dans la majorité des langages, on peut donner une longueur initiale au constructeur des listes tableau afin de donner la capacité initiale du tableau afin d’éviter que trop de copies soient effectuées.
En général, on utilise une liste tableau dans le cas où nous savons la taille nécessaire (ou généralement nécessaire) au travail de la liste.
La documentation Java de la classe « ArrayList » est ici.
La documentation Eiffel de la classe « ARRAYED_LIST » est ici
Notez que vous pouvez voir plusieurs implémentations de Liste tableau dans les exemples ci-dessus.
Les listes liées
Une liste liée (ou « Linked list ») est une liste créée à partir de structures appelées noeud liées entre eux par des pointeurs.
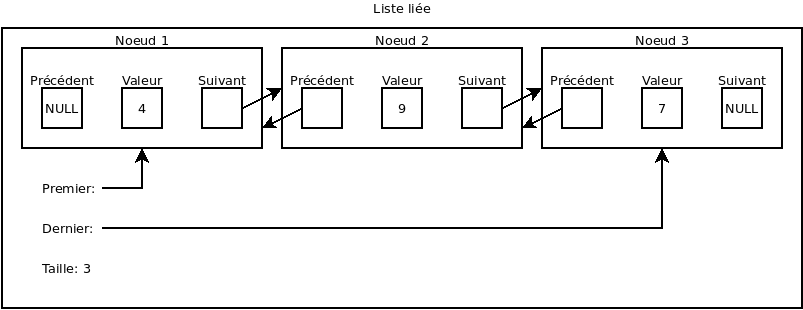
Les listes liées ont beaucoup d’inconvénients par rapport aux listes tableau. En premier lieu, chaque élément prend plus de place que dans le cas d’une liste tableau (en plus de la valeur, il fait stocker les pointeurs dans chaque noeud). De manière encore plus importante, accéder un élément par index est très peu performant puisque la liste doit traverser la liste (une complexité algorithmique de O(n)).
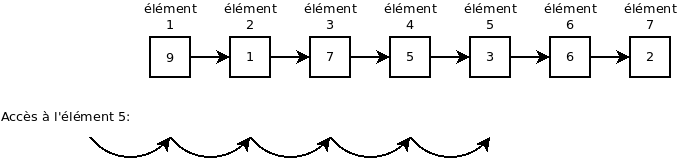
L’avantage majeur d’une liste liée est lorsque la taille maximale de la liste n’est pas connue à priori. L’insertion et la suppression se font en temps constant (ordre de complexité d’ordre O(1)).
On utilise généralement une liste liée lorsqu’il est impossible de savoir la taille maximale que la liste aura lors de l’exécution (ou lorsque la taille maximale est très rarement atteinte et que la taille généralement utilisée n’est pas prévisible).
La documentation Java de la classe « LinkedList » est ici.
La documentation Eiffel de la classe « LINKED_LIST » est ici
Puisque les listes liées, tout comme les listes tableau, respectent l’interface publique de la liste, vous pouvez voir un exemple d’utilisation d’une liste liée en modifiant les listes tableaux dans les exemples ci-haut par des listes liées.
Par exemple, en Java:
/**
* Exécution de l'exemple.
*/
public void execute(){
List<String> lListe = new LinkedList<String>();
lListe.add("Element 1");
lListe.add("Element 2");
lListe.add("Element 3");
lListe.add("Element 4");
lListe.add("Element 5");
lListe.add("Element 6");
lListe.add("Element 7");
lListe.add("Element 8");
lListe.add("Element 9");
lListe.add("Element 10");
printListe(lListe);
}
Un exemple en Eiffel:
make
-- Exécute l'exemple
local
l_liste:LINKED_LIST[STRING]
do
create l_liste.make
l_liste.extend ("Element 1")
l_liste.extend ("Element 2")
l_liste.extend ("Element 3")
l_liste.extend ("Element 4")
l_liste.extend ("Element 5")
l_liste.extend ("Element 6")
l_liste.extend ("Element 7")
l_liste.extend ("Element 8")
l_liste.extend ("Element 9")
l_liste.extend ("Element 10")
print_from_iterable(l_liste)
end
Les distributeurs
On appelle distributeur (ou « dispenser ») une structure abstraite permettant d’y déposer un élément à la fois et d’avoir accès à un élément à la fois (l’élément doit être retiré pour avoir accès à un autre élément).
Les distributeurs sont parfois appelés des sacs (ou « bag ») parce que leurs utilisations ressemblent un peu à un sac de piges. On place des éléments dans le sac et on les retire les un après les autres. Pour observer un élément, il faut le retirer.
L’implémentation des distributeurs se fait généralement avec des structures liées entre elles par des pointeurs (similaire aux listes liées).
Il est à noter que le langage Java n’a pas de classe abstraite représentant ce type de structure.
La documentation de la classe Eiffel « DISPENSER » est ici
Voici un exemple d’utilisation de distributeur en Eiffel:
remplir_dispenser(a_dispenser:DISPENSER[STRING])
-- Ajoute des éléments dans `a_dispenser'
do
a_dispenser.extend ("Element 1")
a_dispenser.extend ("Element 2")
a_dispenser.extend ("Element 3")
a_dispenser.extend ("Element 4")
a_dispenser.extend ("Element 5")
a_dispenser.extend ("Element 6")
a_dispenser.extend ("Element 7")
a_dispenser.extend ("Element 8")
a_dispenser.extend ("Element 9")
a_dispenser.extend ("Element 10")
end
afficher_dispenser(a_dispenser:DISPENSER[STRING])
-- Affiche et vide les éléments de `a_dispenser'
do
from until a_dispenser.is_empty loop
print(a_dispenser.item + "%N")
a_dispenser.remove
end
end
Pour exécuter cet exemple, nous utiliserons les exemples de Pile et de File que nous verrons ensuite.
Les files
Une file (ou « queue ») est un distributeur utilisant un algorithme de type « premier entré, premier sorti » (ou « FIFO » pour « First In, First Out »).
Pour visualiser cet algorithme, on peut imaginer une file de personnes qui attendent à une caisse. Généralement, la première personne à être arrivé dans la file sera la première personne à passer à la caisse (à être retiré de la file).
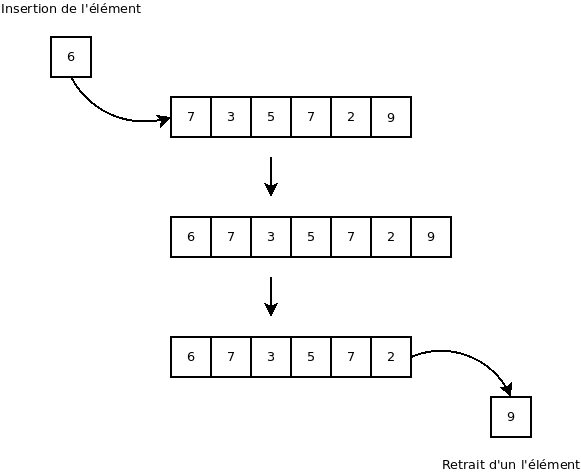
La documentation de « Queue » en Java est ici
La documentation de « QUEUE » en Eiffel est ici
Voici un exemple d’utilisation de File en Java:
/**
* Ajoute des éléments à une file.
*
* @param aFile La structure à ajouter les éléments.
*/
public void remplirFile(Queue<String> aFile) {
aFile.add("Element 1");
aFile.add("Element 2");
aFile.add("Element 3");
aFile.add("Element 4");
aFile.add("Element 5");
aFile.add("Element 6");
aFile.add("Element 7");
aFile.add("Element 8");
aFile.add("Element 9");
aFile.add("Element 10");
}
/**
* Affiche et vide les éléments d'une file.
*
* @param aFile La structure à afficher.
*/
public void afficherFile(Queue<String> aFile) {
while (aFile.peek() != null){
System.out.println(aFile.element());
aFile.remove();
}
}
/**
* Exécution de l'exemple.
*/
public void execute(){
Queue<String> lFile = new ArrayDeque<String>();
remplirFile(lFile);
afficherFile(lFile);
}
L’exemple d’utilisation en Eiffel utilisera les méthodes développé dans la section « distributeur » (les méthodes « remplir_dispenser » et « afficher_dispenser »:
make
-- Exécute l'exemple
local
l_queue:LINKED_QUEUE[STRING]
do
create l_queue.make
remplir_dispenser(l_queue)
afficher_dispenser(l_queue)
end
Le résultat des codes Java et Eiffel ci-dessus est:
Element 1 Element 2 Element 3 Element 4 Element 5 Element 6 Element 7 Element 8 Element 9 Element 10
Les piles
Une pile (ou « stack ») est un distributeur utilisant un algorithme de type « dernier entré, premier sorti » (ou « LIFO » pour « Last In, First Out »).
Pour visualiser cet algorithme, on peut imaginer une pile d’assiettes. Généralement, on prend l’assiette qui est sur le dessus de la pile et lorsqu’on dépose une assiette, on la dépose sur la pile.
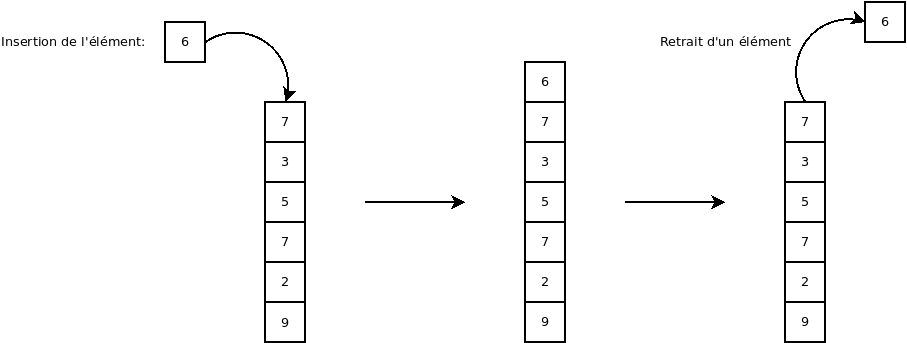
La documentation Java de « Stack » est ici
La documentation Eiffel de « STACK » est ici
Voici un exemple d’utilisation d’une pile en Java:
/**
* Ajoute des éléments à une pile.
*
* @param aPile La structure à ajouter les éléments.
*/
public void remplirPile(Stack<String> aPile) {
aPile.push("Element 1");
aPile.push("Element 2");
aPile.push("Element 3");
aPile.push("Element 4");
aPile.push("Element 5");
aPile.push("Element 6");
aPile.push("Element 7");
aPile.push("Element 8");
aPile.push("Element 9");
aPile.push("Element 10");
}
/**
* Affiche et vide les éléments d'une pile.
*
* @param aPile La structure à afficher.
*/
public void afficherPile(Stack<String> aPile) {
while (!aPile.empty()){
System.out.println(aPile.peek());
aPile.pop();
}
}
/**
* Exécution de l'exemple.
*/
public void execute(){
Stack<String> lPile = new Stack<String>();
remplirPile(lPile);
afficherPile(lPile);
}
L’exemple d’utilisation en Eiffel utilisera les méthodes développées dans la section « distributeur » (les méthodes « remplir_dispenser » et « afficher_dispenser »:
make
-- Exécute l'exemple
local
l_stack:LINKED_STACK[STRING]
do
create l_stack.make
remplir_dispenser(l_stack)
afficher_dispenser(l_stack)
end
Le résultat des codes Java et Eiffel ci-dessus est:
Element 10 Element 9 Element 8 Element 7 Element 6 Element 5 Element 4 Element 3 Element 2 Element 1
Sac aléatoire
Un sac aléatoire (ou « Random Bag » ou « Random Queue ») est un distributeur dans lequel l’élément qui est lu et retiré est choisi au hasard dans le distributeur.
Il est important de comprendre que tant que l’élément n’est pas retiré, l’élément lu ne doit pas changer. La seule façon de modifier l’élément à lire est de retirer l’élément en question.
L’implémentation d’un sac aléatoire n’est pas incluse dans Java ni dans Eiffel. Son implémentation est laissée en exercice aux plus courageux.
Les « buffers » circulaires
Une file est une structure très utile, mais dans certains contextes, elle peut être lourde à implémenter. En effet, lorsqu’un programme est fait dans un environnement bas niveau (langage C ou assembleur, programmation de microcontrôleur, etc.) ou lorsque la performance est un élément clé du programme, on peut remplacer une file par un « buffer » circulaire.
Le « buffer » se comporte normalement comme une file (algorithme FIFO). Par contre, contrairement à une file, le « buffer » circulaire est limité en taille. Il s’agit donc d’une sorte de file pouvant contenir un nombre maximal d’éléments.
Voici comment on implémente un « buffer » circulaire:
-
- Structure:
- Les valeurs sont placées dans un tableau mémoire (« Array »);
- On utilise deux index:
- Tête: Corresponds à l’endroit où nous déposerons nos valeurs;
- Queue: Corresponds à l’endroit où nous allons lire et retirer les valeurs;
- Utilisation:
- Initialement, la tête et la queue sont égales;
- Si « Tête » = « Queue », le « buffer » est vide.
- Lorsqu’une valeur est ajoutée dans le « buffer », on place cette valeur à l’index « Tête » dans le tableau et on incrémente cet index;
- Si « Tête » + 1 = « Queue », le « buffer » est plein.
- Lorsqu’une valeur est retirée du « buffer », on incrémente l’index « Queue »;
- Lorsqu’un index sort du tableau, ce pointeur est redirigé au début du tableau à l’aide d’un modulo.
- Initialement, la tête et la queue sont égales;
- Structure:
Voici un exemple d’utilisation de « buffer » circulaire. Le tableau à l’intérieur du « buffer » est de taille 7.
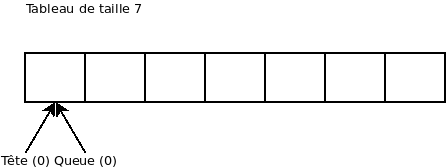
On ajoute la valeur 5:
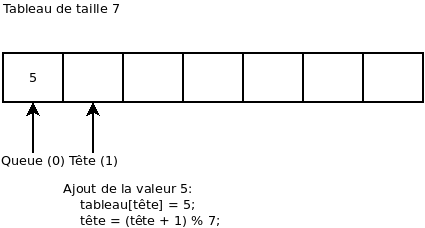
On ajoute la valeur 9:
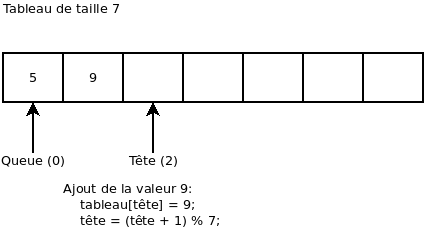
On ajoute la valeur 4:
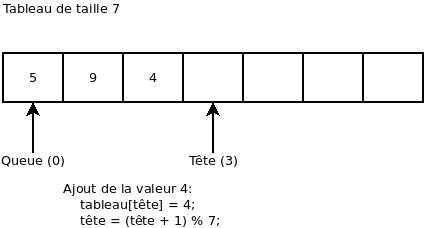
On retire une valeur. Ça nous retourne la valeur 5:
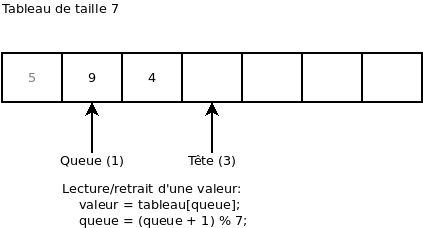
On ajoute 3 valeurs (8, 6, et 1):
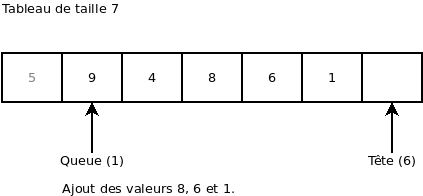
On ajoute la valeur 3. On remarque que l’index « Tête » est retourné au début du tableau:
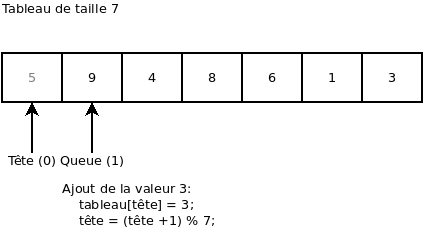
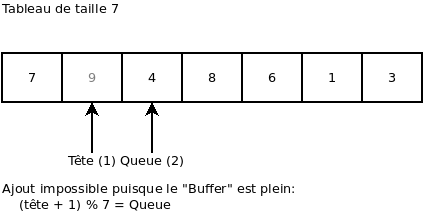
On essaie d’ajouter une valeur (ça donne une erreur, car le « buffer » est plein):
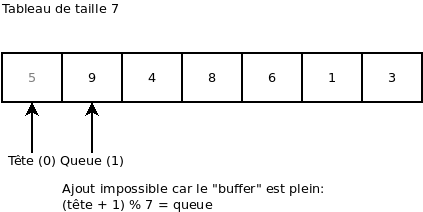
On retire une valeur. Ça nous retourne la valeur 9:
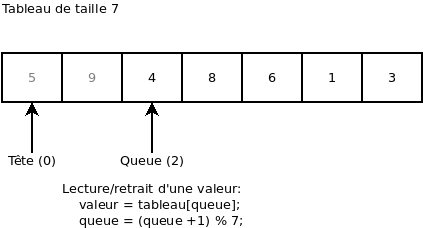
Maintenant que le « buffer » n’est plus plein, on peut ajouter la valeur 7:
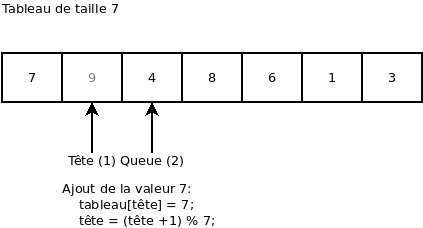
On essaie d’ajouter une valeur (ça donne une erreur, car le « buffer » est plein):
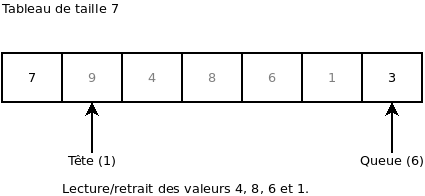
On retire 4 valeurs. Ça nous retourne en ordre les valeurs 4, 8, 6 et 1:
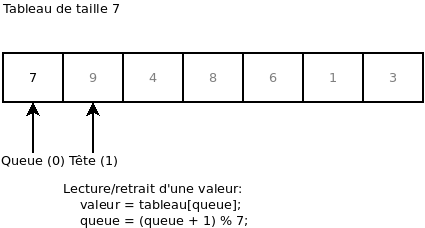
On retire de nouveau une valeur. Ça nous retourne la valeur 3. De plus, on remarque que l’index « Queue » est retourné au début:
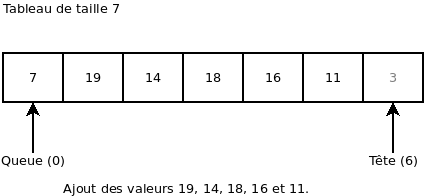
On ajoute les valeurs 19, 14, 18, 16 et 11:
On essaie d’ajouter une valeur (ça donne une erreur, car le « buffer » est plein). En effet, même si la « Tête » est à 6 et la « Queue » est à 0, on a que « Tête » + 1 = « Queue » si nous prenons en compte le modulo. Plus formellement: (« Tête » + 1) modulo 7 = « Queue ».
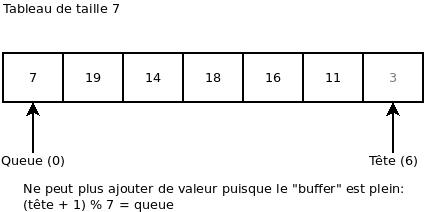
Pour terminer, si nous lisons les éléments 7, 19, 14, 18, 16 et 11 et ce, sans ajouter aucun élément, nous nous retrouvons encore une fois avec « Tête = Queue », ce qui signifie que le « buffer » est maintenant vide.
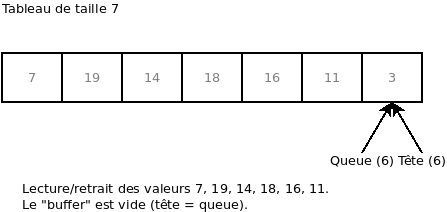
Voici un exemple dans le langage C:
/**
* @author : Louis Marchand (prog@tioui.com)
* @created : mardi sep 07, 2021 20:43:01 EDT
* @license : MIT
*/
#include <stdbool.h>
#include <stdlib.h>
#include <stdio.h>
#define BUFFER_TAILLE 7
/**
* Le buffer circulaire.
*/
typedef struct Buffer {
int donnees[BUFFER_TAILLE];
int tete;
int queue;
bool erreur;
} Buffer;
/**
* Retourne un nouveau buffer circulaire (on null si erreur).
*
* @return Un nouveau buffer circulaire ou null.
*/
Buffer* initialiser_buffer()
{
return calloc(1, sizeof(Buffer));
}
/**
* Retourne Vrai si une erreur est survenue; Faux sinon.
*
* @param a_buffer le buffer circulaire à traiter.
* @return Vrai si une erreur est survenue; Faux sinon.
*/
bool a_erreur(Buffer* a_buffer)
{
return a_buffer->erreur;
}
/**
* Retourne Vrai si le buffer est vide; Faux sinon.
*
* @param a_buffer le buffer circulaire à traiter.
* @return Vrai si le buffer est vide; Faux sinon.
*/
bool est_vide(Buffer* a_buffer)
{
return a_buffer->tete == a_buffer->queue;
}
/**
* Retourne Vrai si le buffer est plein; Faux sinon.
*
* @param a_buffer le buffer circulaire à traiter.
* @return Vrai si le buffer est plein; Faux sinon.
*/
bool est_plein(Buffer* a_buffer)
{
return (a_buffer->tete + 1) % BUFFER_TAILLE == a_buffer->queue;
}
/**
* Ajoute un élément dans le buffer circulaire.
*
* @param a_buffer le buffer circulaire à traiter.
* @param a_element L'élément à placer dans le buffer circulaire.
*/
void ajouter_buffer(Buffer* a_buffer, int a_element)
{
if(!est_plein(a_buffer)) {
a_buffer->donnees[a_buffer->tete] = a_element;
a_buffer->tete = (a_buffer->tete + 1) % BUFFER_TAILLE;
a_buffer->erreur = false;
} else {
a_buffer->erreur = true;
}
}
/**
* Retourne le prochain élément à traiter dans le buffer circulaire.
*
* @param a_buffer le buffer circulaire à traiter.
* @return L'élément à traiter dans le buffer circulaire.
*/
int element_buffer(Buffer* a_buffer)
{
int resultat = 0;
if(!est_vide(a_buffer)) {
resultat = a_buffer->donnees[a_buffer->queue];
a_buffer->erreur = false;
} else {
a_buffer->erreur = true;
}
return resultat;
}
/**
* Retire le prochain élément à traiter dans le buffer circulaire.
*
* @param a_buffer le buffer circulaire à traiter.
*/
void retirer_buffer(Buffer* a_buffer)
{
if(!est_vide(a_buffer)) {
a_buffer->queue = (a_buffer->queue + 1) % BUFFER_TAILLE;
a_buffer->erreur = false;
} else {
a_buffer->erreur = true;
}
}
/**
* Programme principal.
*/
int main(int argc, char *argv[])
{
Buffer* l_buffer = initialiser_buffer();
if (l_buffer != NULL) {
ajouter_buffer(l_buffer, 5);
ajouter_buffer(l_buffer, 9);
ajouter_buffer(l_buffer, 4);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
ajouter_buffer(l_buffer, 8);
ajouter_buffer(l_buffer, 6);
ajouter_buffer(l_buffer, 1);
ajouter_buffer(l_buffer, 3);
ajouter_buffer(l_buffer, 5);
if (a_erreur(l_buffer)) {
printf("Ne peut ajouter un element; le buffer est plein.\n");
}
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
ajouter_buffer(l_buffer, 7);
ajouter_buffer(l_buffer, 5);
if (a_erreur(l_buffer)) {
printf("Ne peut ajouter un element; le buffer est plein.\n");
}
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
ajouter_buffer(l_buffer, 19);
ajouter_buffer(l_buffer, 14);
ajouter_buffer(l_buffer, 18);
ajouter_buffer(l_buffer, 16);
ajouter_buffer(l_buffer, 11);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
printf("Valeur 1 = %d\n", element_buffer(l_buffer));
retirer_buffer(l_buffer);
element_buffer(l_buffer);
if (a_erreur(l_buffer)) {
printf("Ne peut pas voir l'element; le buffer est vide.\n");
}
retirer_buffer(l_buffer);
if (a_erreur(l_buffer)) {
printf("Ne peut retirer l'element; le buffer est vide.\n");
}
} else {
printf("Erreur, ne peut créer le buffer.\n");
}
return 0;
}
Les graphes
Un graphe consiste en des noeuds reliés entre eux par des arrêtes.
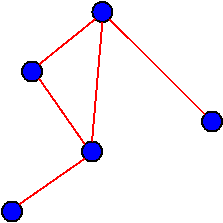
Ici, les noeuds sont représentés par des ronds bleus et les arrêtes sont représentées par les lignes rouges.
Les graphes évalués
Les noeuds (ou les arrêtes) peuvent contenir des valeurs. Dans ce cas, on considère le graphe comme étant évalué.
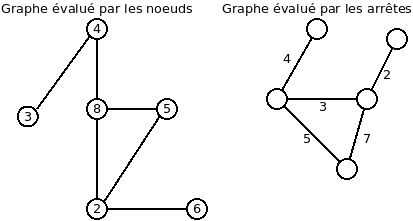
Les graphes orientés
On dit qu’un graphe est orienté lorsque chaque arrêtes contient une direction.
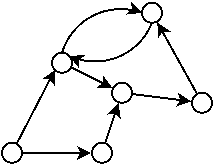
Les graphes cycliques et acycliques
On appel cycle lorsqu’il est possible de repasser par le même noeud plusieurs fois en suivant les arrêtes, sans emprunter plus d’une fois une arrête.
On dit qu’un graphe est cyclique lorsqu’il possède un ou plusieurs cycles.
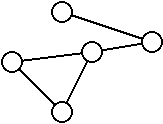
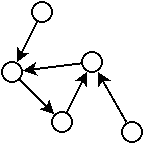
Les exemples précédents sont des graphes cycliques.
De la même manière, on appelle graphe acyclique un graphe ne possédant pas de cycle.
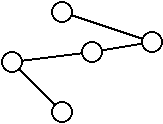
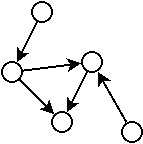
Les exemples précédents sont des graphes acycliques.
Remarquez que dans le second exemple, le graphe semble avoir un cycle, mais il n’en a pas puisque pour suivre une arrête, il faut respecter sa direction.
Les tenants
On appel tenant un sous-ensemble d’un graphe qui n’est relié au reste du graphe par aucune arrête.
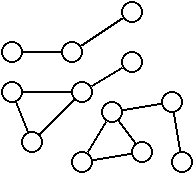
Dans cet exemple, le graphe contient 3 tenants.
Les graphes connexes
On dit qu’un graphe est connexe lorsqu’il contient seulement un seul tenant.
Implémentation d’un graphe
L’implémentation d’un graphe peut varier en fonction du type de graphe utilisé, mais il s’agit généralement d’une liste de noeuds reliés entre eux par des pointeurs représentant les arrêtes.
Puisque, contrairement aux différentes structures vues plus haut, les graphes ne sont pas toujours accessibles via des librairies, je vais donner deux exemples d’implémentation de graphe. Les deux exemples créés le graphe ci-dessous:
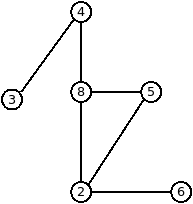
Voici l’exemple Java (nécessite trois (3) fichiers):
Java: Fichier « Noeud.java »:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**
* Représente un élément d'un graphe
* @author Louis Marchand
* @version %I%, %G%
*/
public class Noeud {
/**
* Initialisation du Noeud
*
* @param aValeur La valeur associé au Noeud
* @see #valeur
* @see #getValeur
*/
public Noeud(int aValeur) {
super();
valeur = aValeur;
voisins = new LinkedList<Noeud>();
}
/**
* La valeur associée au Noeud
*/
private int valeur;
/**
* Assigne la valeur associée au Noeud
*
* @param aValeur La valeur à associer
*/
public void setValeur(int aValeur) {
valeur = aValeur;
}
/**
* Retourne la valeur associée au Noeud
*
* @return La valeur;
*/
public int getValeur() {
return valeur;
}
/**
* Les différents Noeuds reliés au Noeud par une arrête
*/
private LinkedList<Noeud> voisins;
/**
* Retourne les différents Noeuds reliés au Noeud par une arrête
*
* @return Les Noeuds voisins
*/
public List<Noeud> getVoisins() {
return new ArrayList<Noeud> (voisins);
}
/**
* Ajoute un Noeud à la liste des voisins du Noeud
* @param aVoisin Le Noeud à ajouter
* @see #voisin
* @see #getVoisin
* @see #retirerVoisin
*/
protected void ajouterVoisin(Noeud aVoisin) {
voisins.add(aVoisin);
}
/**
* Retire un Noeud à la liste des voisins du Noeud
* @param aVoisin Le Noeud à retirer
* @see #voisin
* @see #getVoisin
* @see #ajouterVoisin
*/
protected void retirerVoisin(Noeud aVoisin) {
voisins.remove(aVoisin);
}
}
Fichier « Graphe.java »:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**
* En ensemble de Noeuds reliés par des arrêtes
* @author Louis Marchand
* @version %I%, %G%
*/
public class Graphe {
/**
* Initialisation du Graphe
*/
public Graphe() {
super();
noeuds = new LinkedList<Noeud>();
}
/**
* Tous les Noeuds du Graphe
*/
private LinkedList<Noeud> noeuds;
/**
* Retourne tous les Noeuds du Graphe
*
* @return Les Noeuds du Graphe
*/
public List<Noeud> getNoeuds() {
return new ArrayList<Noeud>(noeuds);
}
/**
* Ajoute un nouveau Noeud dans le Graphe
*
* Ajoute un nouveau Noeud dans les noeuds du Graphe et permet d'accéder
* à ce Noeud par getDernierNoeudAjoute;
*
* @param aValeur La valeur du nouveau Noeud
* @see #getDernierNoeudAjoute
*/
public void ajouterNoeud(int aValeur) {
Noeud lNoeud;
lNoeud = new Noeud(aValeur);
noeuds.add(lNoeud);
dernierNoeudAjoute = lNoeud;
}
/**
* Le dernier Noeud ajouté au Graphe par le méthode ajouterNoeud.
*
* @see #ajouterNoeud
*/
private Noeud dernierNoeudAjoute;
/**
* Retourne le dernier Noeud ajouté au Graphe par la méthode ajouterNoeud.
*
* @return Le Noeud ajouté
* @see #ajouterNoeud
*/
public Noeud getDernierNoeudAjoute() {
return dernierNoeudAjoute;
}
/**
* Ajoute une arrête entre deux noeuds.
*
* @param aNoeud1 Le premier Noeud
* @param aNoeud2 Le second Noeud
*/
public void creerArrete(Noeud aNoeud1, Noeud aNoeud2) {
aNoeud1.ajouterVoisin(aNoeud2);
aNoeud2.ajouterVoisin(aNoeud1);
}
/**
* Retire une arrête entre deux noeuds.
*
* @param aNoeud1 Le premier Noeud
* @param aNoeud2 Le second Noeud
*/
public void retirerArrete(Noeud aNoeud1, Noeud aNoeud2) {
aNoeud1.retirerVoisin(aNoeud2);
aNoeud2.retirerVoisin(aNoeud1);
}
}
Fichier « Programme.java »:
/**
* Exemple de programme utilisant des graphes.
* @author Louis Marchand
* @version %I%, %G%
*/
public class Programme {
/**
* Exécution du Programme principal.
*
* @param aArguments Les arguments qui on été passé au Programme.
*/
public static void main(String[] aArguments) {
Graphe lGraphe = new Graphe();
Noeud lNoeud1, lNoeud2, lNoeud3, lNoeud4, lNoeud5, lNoeud6;
lGraphe.ajouterNoeud(4);
lNoeud1 = lGraphe.getDernierNoeudAjoute();
lGraphe.ajouterNoeud(3);
lNoeud2 = lGraphe.getDernierNoeudAjoute();
lGraphe.creerArrete(lNoeud1, lNoeud2);
lGraphe.ajouterNoeud(8);
lNoeud3 = lGraphe.getDernierNoeudAjoute();
lGraphe.creerArrete(lNoeud1, lNoeud3);
lGraphe.ajouterNoeud(2);
lNoeud4 = lGraphe.getDernierNoeudAjoute();
lGraphe.creerArrete(lNoeud3, lNoeud4);
lGraphe.ajouterNoeud(6);
lNoeud5 = lGraphe.getDernierNoeudAjoute();
lGraphe.creerArrete(lNoeud4, lNoeud5);
lGraphe.ajouterNoeud(5);
lNoeud6 = lGraphe.getDernierNoeudAjoute();
lGraphe.creerArrete(lNoeud3, lNoeud6);
lGraphe.creerArrete(lNoeud4, lNoeud6);
}
}
Voici le même exemple en Eiffel (toujours trois fichiers nécessaires):
Fichier « noeud.e »:
note
description: "Représente un élément d'un graphe"
auteur: "Louis Marchand"
date: "Mon, 28 Sep 2020 20:27:40 +0000"
revision: "0.1"
class
NOEUD
create
make
feature {NONE} -- Initialisation
make(a_valeur:INTEGER)
-- Initialisation de `Current'
do
valeur := a_valeur
create {LINKED_LIST[NOEUD]} voisins_interne.make
end
feature -- Accès
valeur:INTEGER assign set_valeur
-- La valeur associée à `Current'
set_valeur(a_valeur:INTEGER)
-- Assigne `valeur' avec `a_valeur'
do
valeur := a_valeur
end
voisins:LIST[NOEUD]
-- Les différents {NOEUD} reliés à `Current' par une arrête
do
Result := voisins_interne.twin
end
feature {GRAPHE} -- Implémentation
ajouter_voisin(a_voisin:NOEUD)
-- Ajoute `a_voisin' dans la liste de `voisins'
do
voisins_interne.extend (a_voisin)
end
retirer_voisin(a_voisin:NOEUD)
-- Enlève `a_voisin' de la liste de `voisins'
do
voisins_interne.prune_all (a_voisin)
end
feature {NONE} -- Implémentation
voisins_interne:LIST[NOEUD]
-- Représentation interne de `voisin'
end
Fichier « graphe.e »:
note
description: "En ensemble de {NOEUD} reliés par des arrêtes"
auteur: "Louis Marchand"
date: "Mon, 28 Sep 2020 20:27:40 +0000"
revision: "0.1"
class
GRAPHE
create
make
feature {NONE} -- Initialisation
make
-- Initalisation de `Current'
do
create {LINKED_LIST[NOEUD]}noeuds_interne.make
end
feature -- Access
noeuds:LIST[NOEUD]
-- La liste des {NOEUD} de `Current'
do
Result := noeuds_interne.twin
end
ajouter_noeud(a_valeur:INTEGER)
-- Ajoute un nouveau {NOEUD} en utilisant `a_valeur' comme `valeur'
local
l_noeud:NOEUD
do
create l_noeud.make (a_valeur)
dernier_noeud_ajoute := l_noeud
noeuds_interne.extend (l_noeud)
end
dernier_noeud_ajoute:detachable NOEUD
-- Le dernier {NOEUD} qui a été ajouté par `ajouter_noeud'
creer_arrete(a_noeud1, a_noeud_2:NOEUD)
-- Ajoute un arrête entre `a_noeud_1' et `a_noeud_2'
do
a_noeud1.ajouter_voisin (a_noeud_2)
a_noeud_2.ajouter_voisin (a_noeud1)
end
retirer_arrete(a_noeud1, a_noeud_2:NOEUD)
-- Retire un arrête entre `a_noeud_1' et `a_noeud_2'
do
a_noeud1.retirer_voisin (a_noeud_2)
a_noeud_2.retirer_voisin (a_noeud1)
end
feature {NONE} -- Implémentation
noeuds_interne:LIST[NOEUD]
-- Représentation interne de `noeuds'
end
Fichier « application.e »:
note
description: "Application exemple pour démontrer l'implémentation des graphes"
auteur: "Louis Marchand"
date: "Mon, 28 Sep 2020 20:27:40 +0000"
revision: "0.1"
class
APPLICATION
create
make
feature {NONE} -- Initialization
make
-- Exécute l'application.
local
l_graphe:GRAPHE
do
create l_graphe.make
l_graphe.ajouter_noeud (4)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_1 then
l_graphe.ajouter_noeud (3)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_2 then
l_graphe.creer_arrete (la_noeud_1, la_noeud_2)
end
l_graphe.ajouter_noeud (8)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_3 then
l_graphe.creer_arrete (la_noeud_1, la_noeud_3)
l_graphe.ajouter_noeud (2)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_4 then
l_graphe.creer_arrete (la_noeud_3, la_noeud_4)
l_graphe.ajouter_noeud (6)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_5 then
l_graphe.creer_arrete (la_noeud_4, la_noeud_5)
end
l_graphe.ajouter_noeud (5)
if attached l_graphe.dernier_noeud_ajoute as la_noeud_6 then
l_graphe.creer_arrete (la_noeud_3, la_noeud_6)
l_graphe.creer_arrete (la_noeud_4, la_noeud_6)
end
end
end
end
end
end
Parcourir un graphe
Puisqu’un graphe peut avoir plusieurs tenants et peut également avoir un des cycles, le parcourir d’un graphe peut-être très difficile à implémenter. Voici donc un exemple de parcourt de graphe. Cette fonction prend en argument un noeud et une valeur et doit retourner vrai dans le cas où la valeur peut être trouvée dans un noeud accessible à partir du noeud reçu en argument.
Exemple en Java:
/**
* Indique si la valeur est accessible dans le graphe.
*
* @param aGraphe Le Graphe dans lequel on recherche.
* @param aValeur La valeur à rechercher
* @return Vrai si la valeur a été trouvé, non sinon.
*/
public boolean trouverValeur(Graphe aGraphe, int aValeur) {
boolean lResultat = false;
Noeud lNoeud;
List<Noeud> lTraite = new LinkedList<Noeud>();
Iterator<Noeud> lNoeudsIterator = aGraphe.getNoeuds().iterator();
while (lNoeudsIterator.hasNext() && !lResultat) {
lNoeud = lNoeudsIterator.next();
if (!lTraite.contains(lNoeud)) {
lResultat = trouverValeurIteration(lNoeud, aValeur, lTraite);
}
}
return lResultat;
}
/**
* Indique si la valeur est accessible dans un noeud à partir d'un noeud.
*
* Noter qu'une liste des noeuds déjà traités est fourni et
* que cette méthode a un effet de bord sur cette liste.
*
* @param aNoeud Le Noeud dans lequel débuter la recherche.
* @param aValeur La valeur à rechercher
* @param aTraite Les noeuds déjà traités
* @return Vrai si la valeur a été trouvé, non sinon.
*/
private boolean trouverValeurIteration(
Noeud aNoeud, int aValeur, List<Noeud> aTraite) {
Iterator<Noeud> lVoisinsIterator;
Noeud lVoisin;
boolean lResultat = false;
aTraite.add(aNoeud);
if (aNoeud.getValeur() == aValeur) {
lResultat = true;
} else {
lVoisinsIterator = aNoeud.getVoisins().iterator();
while (lVoisinsIterator.hasNext() && !lResultat) {
lVoisin = lVoisinsIterator.next();
if (!aTraite.contains(lVoisin)) {
lResultat = trouverValeurIteration(lVoisin, aValeur, aTraite);
}
}
}
return lResultat;
}
Exemple en Eiffel:
trouver_valeur(a_graphe:GRAPHE; a_valeur:INTEGER):BOOLEAN
-- Indique si la valeur est accessible dans `a_graphe'
local
l_noeuds_curseur:ITERATION_CURSOR[NOEUD]
l_traite:LINKED_LIST[NOEUD]
do
create l_traite.make
from
Result := False
l_noeuds_curseur := a_graphe.noeuds.new_cursor
until
l_noeuds_curseur.after or Result
loop
Result := trouver_valeur_iteration(
l_noeuds_curseur.item, a_valeur, l_traite)
l_noeuds_curseur.forth
end
end
trouver_valeur_iteration(
a_noeud:NOEUD; a_valeur:INTEGER; a_traite:LIST[NOEUD]):BOOLEAN
-- Indique si la valeur est accessible dans un {NOEUD} à partir de `a_noeud'
-- considérant que les {NOEUD} de `a_traite' on déjà été traités.
-- Noter que la fonction a un effet de bord sur `a_traite'.
local
l_voisins_curseur:ITERATION_CURSOR[NOEUD]
do
a_traite.extend (a_noeud)
Result := False
if a_noeud.valeur = a_valeur then
Result := True
else
from
l_voisins_curseur := a_noeud.voisins.new_cursor
until
l_voisins_curseur.after or Result
loop
if not a_traite.has (l_voisins_curseur.item) then
Result := trouver_valeur_iteration(
l_voisins_curseur.item, a_valeur, a_traite)
end
l_voisins_curseur.forth
end
end
end
Remarquez que j’en ai également profité pour vous montrer l’utilisation des itérateurs (« ITERATION_CURSOR » en Eiffel). Ça permet de ne pas avoir à garder une copie de la liste en variable. Tout ce dont on a besoin, c’est un itérateur qui parcourra la liste en question. Ça évite d’effectuer des manipulations non souhaitables à la liste.
Les arbres
Un arbre est un graphe connexe, acyclique et orienté. Un arbre peut être évalué ou non.
Lorsqu’on a un arbre non vide, on appel racine le seul noeud n’étant la destination d’aucune arrête.
On appel feuille tous les noeuds n’étant la source d’aucune arrête.
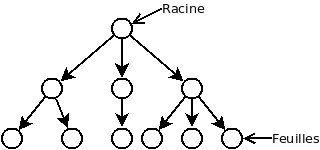
Les restrictions imposées aux arbres font de ces derniers de très bonnes structures pour représenter une structure parent/enfant (où chaque noeud à 0, 1 ou plusieurs enfants et chaque noeud sauf la racine à un seul parent).
Il est à noter que tous les noeuds sont en soi la racine d’un sous-arbre. La récursion est donc une méthode importante dans l’utilisation des arbres.
Malgré que l’implémentation d’un arbre est plus simple que pour le graphe, il n’en demeure pas moins qu’il s’agit d’une structure qu’il est souvent nécessaire d’implémenter soi-même. De plus, tout comme le graphe, en fonction du type d’arbre que nous désirons utiliser, l’implémentation devra être adaptée. Voici donc un exemple d’implémentation d’arbre. L’arbre produit par les programmes sera le suivant:
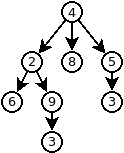
Exemple en Java (deux fichiers nécessaires):
Fichier « Arbre.java »:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
/**
* Structure de graphe connexe, acyclique et orienté.
* @author Louis Marchand
* @version %I%, %G%
*/
public class Arbre {
/**
* Initialisation de l'Arbre.
*
* @param aValeur La valeur assigné à la racine
* @see #valeur
* @see #getValeur
* @see #setValeur
*/
public Arbre(int aValeur){
valeur = aValeur;
enfants = new LinkedList<Arbre>();
}
/**
* La valeur à la racine de l'Arbre.
*/
private int valeur;
/**
* Retourne la valeur de la racine de l'Arbre.
*
* @return La valeur de la racine de l'Arbre.
* @see #setValeur
*/
public int getValeur() {
return valeur;
}
/**
* Assigne la valeur à la racine de l'Arbre.
*
* @param aValeur La valeur à assignée.
* @see #getValeur
*/
public void setValeur(int aValeur) {
valeur = aValeur;
}
/**
* Les sous-arbres de l'Arbre.
*/
private LinkedList<Arbre> enfants;
/**
* Retourne les sous-arbres de l'Arbre.
*
* @return Les sous-arbres de l'Arbre
*/
public List<Arbre> getEnfants() {
return new ArrayList<Arbre>(enfants);
}
/**
* Ajoute un sous-arbre à l'Arbre.
*
* @param aEnfant Le sous-arbre à ajouter
* @see #getEnfants
* @see #retirerEnfant
*/
public void ajouterEnfant(Arbre aEnfant) {
enfants.add(aEnfant);
}
/**
* Retire un sous-arbre de l'Arbre.
*
* @param aEnfant le sous-arbre à retirer
* @see #getEnfants
* @see #ajouterEnfant
*/
public void retirerEnfant(Arbre aEnfant) {
enfants.remove(aEnfant);
}
}
Fichier « Programme.java »:
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Queue;
/**
* Exemple de programme utilisant des arbres.
* @author Louis Marchand
* @version %I%, %G%
*/
public class Programme {
/**
* Exécution du Programme principal.
*
* @param aArguments Les arguments qui on été passé au Programme.
*/
static public void main(String[] aArguments) {
Arbre lArbre = new Arbre(4);
lArbre.ajouterEnfant(new Arbre(2));
lArbre.ajouterEnfant(new Arbre(8));
lArbre.ajouterEnfant(new Arbre(5));
lArbre.getEnfants().get(0).ajouterEnfant(new Arbre(6));
lArbre.getEnfants().get(0).ajouterEnfant(new Arbre(9));
lArbre.getEnfants().get(2).ajouterEnfant(new Arbre(3));
lArbre.getEnfants().get(0).getEnfants().get(1).ajouterEnfant(new Arbre(3));
}
}
Exemple en Eiffel (deux fichiers nécessaires):
Fichier « arbre.e »:
note
description: "Structure de graphe connexe, acyclique et orienté"
author: "Louis Marchand"
date: "Mon, 28 Sep 2020 20:27:40 +0000"
revision: "0.1"
class
ARBRE
create
make
feature {NONE} -- Initialisation
make(a_valeur:INTEGER)
-- Initialisation de `Current' assignant `a_valeur' comme `valeur'
do
valeur := a_Valeur
create {LINKED_LIST[ARBRE]} enfants_interne.make
end
feature --Accès
valeur:INTEGER
-- La valeur à la racine de `Current'
set_valeur(a_valeur:INTEGER)
-- Assigne `valeur' avec `a_valeur'
do
valeur := a_valeur
end
enfants:LIST[ARBRE]
-- Les sous-arbres de `Current'
do
Result := enfants_interne.twin
end
ajouter_enfant(a_arbre:ARBRE)
-- Ajoute `a_arbre' à la liste des `enfants'
do
enfants_interne.extend (a_arbre)
end
retirer_enfant(a_arbre:ARBRE)
-- retire `a_arbre' de la liste des `enfants'
do
enfants_interne.prune_all (a_arbre)
end
feature {NONE} -- Implémentation
enfants_interne:LIST[ARBRE]
-- Représentation interne de `enfants'
end
Fichier « application.e »:
note
description: "Application exemple pour démontrer l'implémentation des arbres"
auteur: "Louis Marchand"
date: "Mon, 28 Sep 2020 20:27:40 +0000"
revision: "0.1"
class
APPLICATION
create
make
feature {NONE} -- Initialization
make
-- Exécute l'application
local
l_arbre:ARBRE
do
create l_arbre.make (4)
l_arbre.ajouter_enfant (create {ARBRE}.make (2))
l_arbre.ajouter_enfant (create {ARBRE}.make (8))
l_arbre.ajouter_enfant (create {ARBRE}.make (5))
l_arbre.enfants[1].ajouter_enfant (create {ARBRE}.make (6))
l_arbre.enfants[1].ajouter_enfant (create {ARBRE}.make (9))
l_arbre.enfants[3].ajouter_enfant (create {ARBRE}.make (3))
l_arbre.enfants[1].enfants[2].ajouter_enfant (create {ARBRE}.make (3))
end
end
Parcours d’un arbre
Il y a deux manières classiques de parcourir un arbre: le parcours en profondeur et le parcours en largeur. L’utilisation d’une ou l’autre des techniques dépends en grande partit de votre préférence ainsi que des contraintes du code dans lequel vous travaillez.
Parcours en profondeur
Le parcours en profondeur descend à travers toutes les branches de l’arbre, les unes à la suite des autres de manière récursive. L’algorithme se rend jusqu’aux feuilles d’une branche avant de se rendre à la prochaine branche. Voici le déplacement qu’effectue le parcours en profondeur. La ligne rouge représente l’ordre de traitement des noeuds.
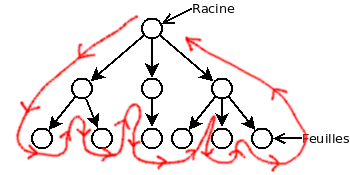
Voici un exemple en Java:
/**
* Effectue une recherche de valeur dans un Arbre.
*
* @param aArbre L'arbre dans lequel chercher.
* @param aValeur La valeur à rechercher dans l'arbre.
* @return true si la valeur est trouvée dans l'arbre. false sinon.
*/
public boolean rechercheProfondeur(Arbre aArbre, int aValeur) {
boolean lResultat = false;
Iterator<Arbre> lEnfantsIterator;
if (aArbre.getValeur() == aValeur) {
lResultat = true;
} else {
lEnfantsIterator = aArbre.getEnfants().iterator();
while (lEnfantsIterator.hasNext() && !lResultat) {
lResultat = rechercheProfondeur(lEnfantsIterator.next(), aValeur);
}
}
return lResultat;
}
Voici le même exemple en Eiffel:
recherche_profondeur(a_arbre:ARBRE; a_valeur:INTEGER):BOOLEAN
-- Retourne `True' si `a_arbre' contient `a_valeur'
do
if a_arbre.valeur = a_valeur then
Result := True
else
Result := across a_arbre.enfants as la_enfants some
recherche_profondeur(la_enfants.item, a_valeur)
end
end
end
Parcours en largeur
Le parcours en largeur traite les noeuds étages par égage. Il s’agit d’un algorithme qui n’est pas récursif et qui nécessite l’utilisation d’une file (« queue »). Voici le déplacement qu’effectue le parcours en profondeur. La ligne rouge représente l’ordre de traitement des noeuds.
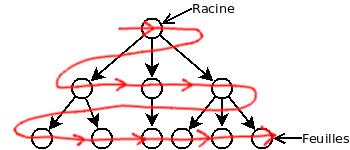
Voici un exemple en Java:
/**
* Effectue une recherche de valeur dans un Arbre.
*
* @param aArbre L'arbre dans lequel chercher.
* @param aValeur La valeur à rechercher dans l'arbre.
* @return true si la valeur est trouvée dans l'arbre. false sinon.
*/
public boolean rechercheLargeur(Arbre aArbre, int aValeur) {
boolean lResultat = false;
Arbre lArbre;
Queue<Arbre> lFile = new LinkedList<Arbre>();
lFile.add(aArbre);
while (!lFile.isEmpty() && !lResultat) {
lArbre = lFile.element();
lFile.remove();
if (lArbre.getValeur() == aValeur) {
lResultat = true;
} else {
lFile.addAll(lArbre.getEnfants());
}
}
return lResultat;
}
Voici le même exemple en Eiffel:
recherche_largeur(a_arbre:ARBRE; a_valeur:INTEGER):BOOLEAN
-- Retourne `True' si `a_arbre' contient `a_valeur'
local
l_file:LINKED_QUEUE[ARBRE]
l_arbre:ARBRE
do
create l_file.make
from
l_file.extend (a_arbre)
Result := False
until
l_file.is_empty or Result
loop
l_arbre := l_file.item
l_file.remove
if l_arbre.valeur = a_valeur then
Result := True
else
l_file.append (l_arbre.enfants)
end
end
end
Les tables de hachage
Une table est une structure indexable, mais contrairement aux listes, l’index (ici appelé clé) peut être n’importe quelle valeur ou type.
Par exemple, voir le code Java suivant:
int[] tableau = new int[10];
tableau[0] = 0; // OK
tableau[9] = 9; // OK
tableau[10] = 10; // Erreur
tableau[19283] = 19283; // Erreur
L’objectif d’une table de hachage est de pouvoir utiliser un code comme ceci:
tableau[0] = 0; // OK
tableau[9] = 9; // OK
tableau[10] = 10; // OK
tableau[19283] = 19283; // OK
Ou même ceci:
tableau[0] = 0; // OK
tableau[9] = 9; // OK
tableau[10] = 10; // OK
tableau["Bonjour"] = 19283; // OK
La fonction de hachage
Afin de pouvoir fonctionner, une table de hachage transfère une valeur quelconque (potentiellement infini et de type quelconque) vers un résultat fini et borné (avec une borne inférieure et supérieure).
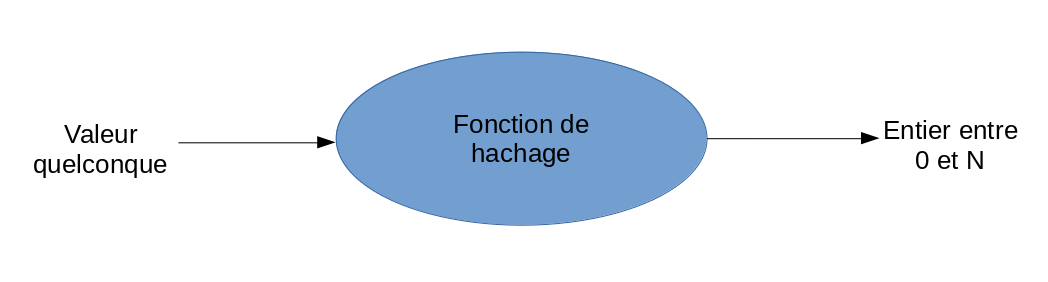
Par exemple, nous pourrions utiliser le restant de la division entière (modulo) comme fonction de hachage.
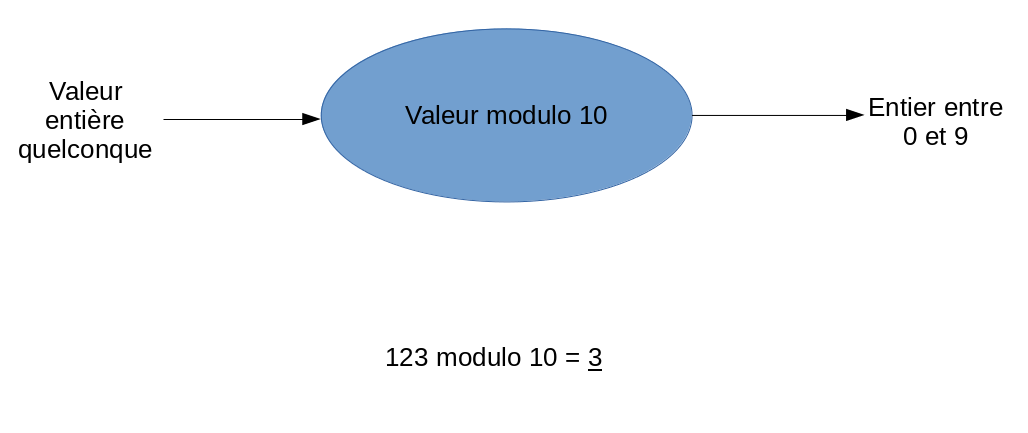
De cette manière, nous pourrions remplacer n’importe quelle clé entière en index entre 0 et 9.
Pour réussir à utiliser comme clé des objets de type autre qu’entier, il faut trouver une manière de transformer cet objet en nombre entier. Par exemple, pour une chaîne de caractère, on pourrait utiliser le code (ASCII, Unicode, etc.) de chaque caractère afin de trouver un nombre entier qui représente la chaîne.
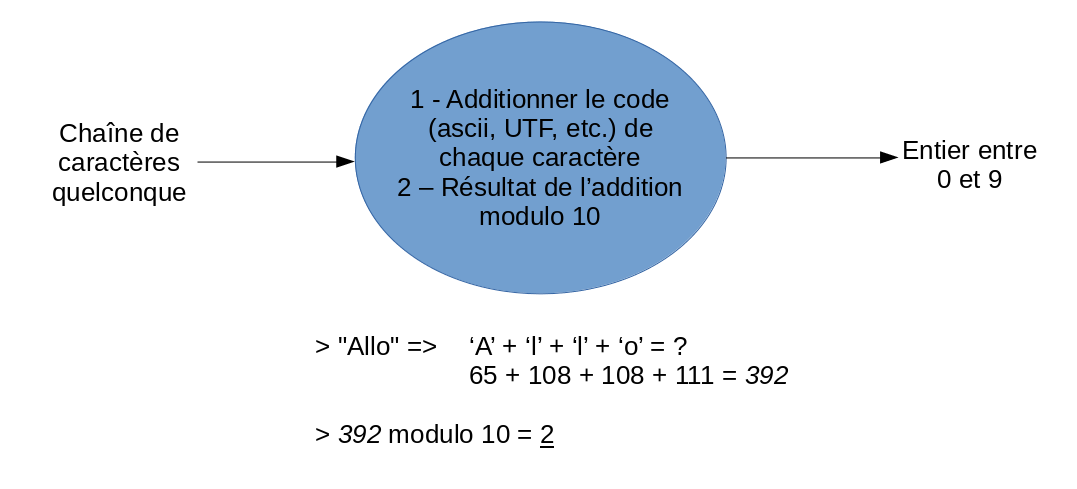
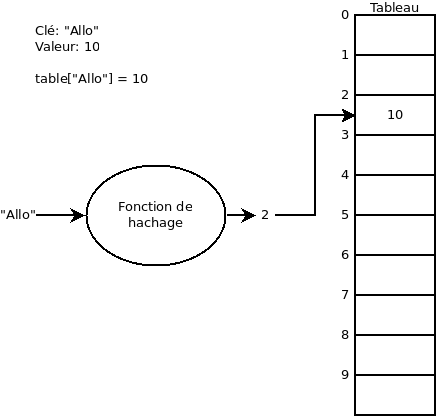
Structure d’une table de hachage
Une fois qu’on a la fonction de hachage, la table utilise un tableau de taille équivalent à l’image (dans le sens mathématique) de la fonction de hachage (par exemple, pour la fonction de hachage « modulo 10 », nous aurons un tableau de taille 10).
Le problème ici, c’est qu’il est possible que la fonction de hachage donne le même résultat pour deux valeurs d’entrées différentes. Dans ce cas, nous avons un conflit puisque deux clés génèrent le même index. Par exemple:
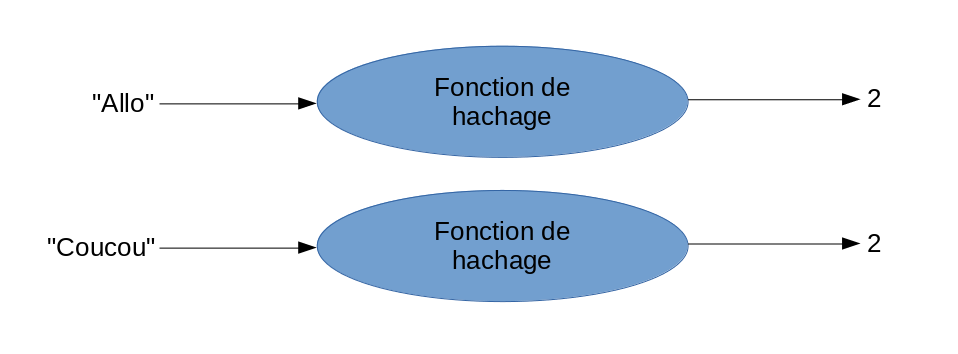
Pour gérer ces conflits, au lieu de placer directement le résultat dans le tableau, le tableau contiendra une liste liée dans chacune de ses cellules pour y stocker l’information.
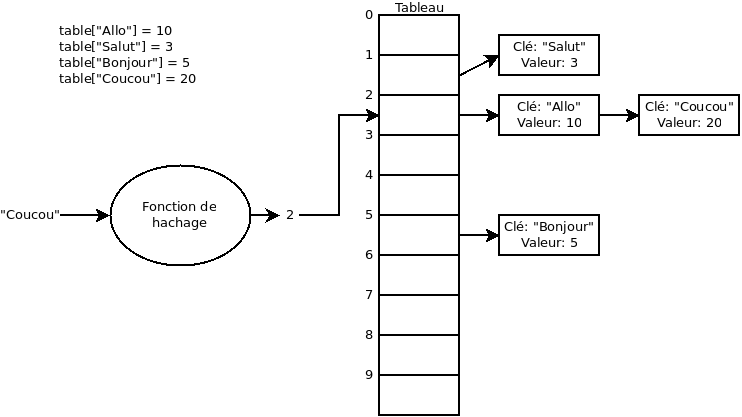
Taille du tableau
Dans la plupart des langages, le constructeur de la table de hachage prend en argument la taille du tableau à utiliser. Cette valeur est très importante, car elle permet d’optimisation l’utilisation de la table de hachage.
En effet, si nous prenons une taille trop grande, la table peut trouver l’élément associé à une clé en temps constant (complexité O(1)), mais de l’espace mémoire est gaspillé. Inversement, si nous prenons une taille trop petite, la table ne gaspille pas d’espace mémoire, mais a la même performance qu’une liste liée (dans le pire cas, on a une complexité de O(n)).
Afin de trouver la meilleure taille de tableau, il est nécessaire d’approximer le nombre d’éléments qui sera placé dans la table lors de l’exécution du programme. Ce que nous cherchons, c’est l’ordre de grandeur. Par exemple, si nous réservons 1000 espaces dans le tableau et que le programme place 10 éléments dans la table, la taille est mal choisie, car 10 et 1000 ne sont pas dans le même ordre de grandeur. Par contre, si on réserve 1000 espaces dans le tableau et que le programme place 2000 éléments dans la table, la taille est bien choisie, car 1000 et 2000 sont dans le même ordre de grandeur.
Il est toute foi à noter que, peu importe le nombre d’espaces de tableau réservés lors de la création de la table et peu importe le nombre d’éléments que le programme placera dans la table, la structure fonctionnera quand même. Une bonne valeur de taille de tableau est une optimisation; rien de plus.
Implémentation
La documentation Java de la classe « Hashtable » est ici.
La documentation Eiffel de la classe « TABLE » est ici.
Voici un exemple d’utilisation d’une table de hachage en Java:
/**
* Exécution de l'exemple.
*/
public void execute(){
Hashtable<String, Integer> lTable = new Hashtable<String, Integer>(10);
lTable.put("Un", Integer.valueOf(1));
lTable.put("Deux", Integer.valueOf(2));
lTable.put("Trois", Integer.valueOf(3));
lTable.put("Quatre", Integer.valueOf(4));
lTable.put("Cinq", Integer.valueOf(5));
lTable.put("Six", Integer.valueOf(6));
lTable.put("Sept", Integer.valueOf(7));
lTable.put("Huit", Integer.valueOf(8));
lTable.put("Neuf", Integer.valueOf(9));
lTable.put("Dix", Integer.valueOf(10));
System.out.println("Valeur de Un: " + lTable.get("Un").toString());
System.out.println("Valeur de Deux: " + lTable.get("Deux").toString());
System.out.println("Valeur de Trois: " + lTable.get("Trois").toString());
System.out.println("Valeur de Quatre: " + lTable.get("Quatre").toString());
System.out.println("Valeur de Cinq: " + lTable.get("Cinq").toString());
System.out.println("Valeur de Six: " + lTable.get("Six").toString());
System.out.println("Valeur de Sept: " + lTable.get("Sept").toString());
System.out.println("Valeur de Huit: " + lTable.get("Huit").toString());
System.out.println("Valeur de Neuf: " + lTable.get("Neuf").toString());
System.out.println("Valeur de Dix: " + lTable.get("Dix").toString());
}
Voici un exemple d’utilisation d’une table de hachage en Eiffel:
make
-- Exécute l'exemple
local
l_table:HASH_TABLE[INTEGER, STRING]
do
create l_table.make(10)
l_table.put (1, "Un")
l_table.put (2, "Deux")
l_table.put (3, "Trois")
l_table.put (4, "Quatre")
l_table.put (5, "Cinq")
l_table.put (6, "Six")
l_table.put (7, "Sept")
l_table.put (8, "Huit")
l_table.put (9, "Neuf")
l_table.put (10, "Dix")
afficher_element_table(l_table, "Un")
afficher_element_table(l_table, "Deux")
afficher_element_table(l_table, "Trois")
afficher_element_table(l_table, "Quatre")
afficher_element_table(l_table, "Cinq")
afficher_element_table(l_table, "Six")
afficher_element_table(l_table, "Sept")
afficher_element_table(l_table, "Huit")
afficher_element_table(l_table, "Neuf")
afficher_element_table(l_table, "Dix")
end
afficher_element_table(a_table:HASH_TABLE[INTEGER, STRING]; a_cle:STRING)
-- Afficher l'élément indexé par `a_cle' dans la table `a_table'
-- si ce dernier existe.
do
if attached a_table.at (a_cle) as la_element then
print("Valeur de " + a_cle + ": " + la_element.out + "%N")
end
end
Auteur: Louis Marchand

Sauf pour les sections spécifiées autrement, ce travail est sous licence Creative Commons Attribution 4.0 International.